תוכניות לינאריות ואיך בונים קבוצת מדגם

כדי לשכנע את ה-FDA לאשר את האלגוריתמים הרפואיים של זברה, אנחנו צריכים להוכיח להם שהם בטוחים לשימוש על האוכלוסייה האמריקאית. לשם כך עלינו לבחון ולדווח את ביצועי האלגוריתם על קבוצת מדגם (test set) המשקפת עד כמה שניתן את אוכלוסיית החולים שעליה עתיד לעבוד כל אלגוריתם. בנוסף להתאמות דמוגרפיות, כמו למשל התפלגות המין והתפלגות הגילאים, צריך לוודא שב-test set יש ייצוג רחב ככל האפשר לכל מיני תתי מקרים.

למשל, אם אנחנו מחפשים גידול סרטני בתמונת CT, צריך לוודא שבקבוצת החיוביים יש ייצוג לטווח הגדלים השונים של הגידול. גם בקרב הדוגמאות השליליות, צריך להבטיח ייצוג הולם למקרים שליליים "קשים", מאתגרים, למשל של גידולים שפירים שהיינו רוצים שהאלגוריתם לא יתריע עליהם.

בנייה של קבוצת מדגם כזו אשר עומדת בכל הדרישות יכולה לקחת זמן רב (אני אומר זאת מנסיון כואב) בלי כלים מתאימים. בנוסף, בניית קבוצות מדגם היא תהליך דינאמי המלווה את הפרוייקט לכל אורכו, הן מכיוון שהגדרות האילוצים על קבוצת המדגם עשויות להשתנות במהלך הפרוייקט (למשל כדי לכלול מקור דאטה חדש), והן משום שנדרשות קבוצות מדגם לשימוש פנימי (validation set, tuning set), או עבור use cases שונים של המוצר.

בפוסט הזה אני רוצה לתאר לכם כלי כזה שבנינו בזברה מדיקל, שהופך את בניית קבוצת המדגם לעניין של דקות.

בניית קבוצת המדגם

אנו מתחילים עם מאגר הדוגמאות שעומד לרשותנו, אשר יכול לכלול אלפי או עשרות-אלפי דוגמאות. נארגן את הנתונים עליהם כך שכל דוגמה כזו תופיע כשורה בטבלה. הנה השורות הראשונות בטבלה כזו, שמציגה את רשימת הנוסעים על הטיטניק (הטור Survived הוא 1 אם הנוסע שרד):

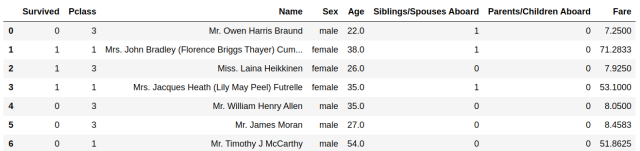
טבלה 1: רשימת הנוסעים על הטיטאניק, סוג ומחיר הכרטיס ששילמו, והאם שרדו את האסון.

בטבלה נוספת, ננסח את התנאים שאנחנו רוצים שקבוצת המדגם תעמוד בהם:

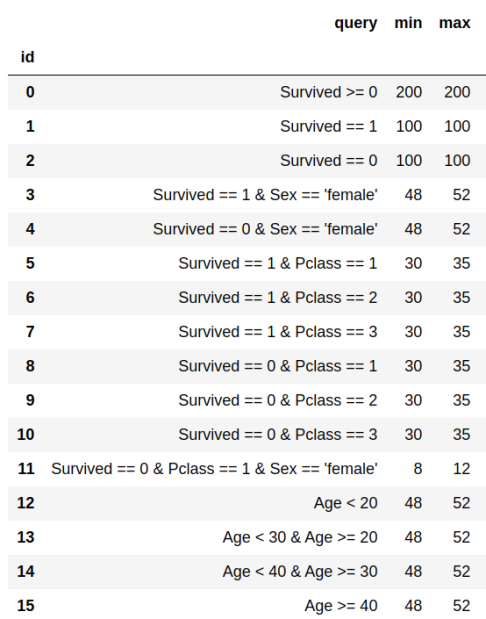
טבלה 2: האילוצים הנדרשים על קבוצת המדגם. כל אילוץ מוצג כשאילתא על טבלה 1, ומצויין כמה (טווח) נוסעים שעונים על השאילתא מותר לקחת אל קבוצת המדגם.

הטבלה הזו אומרת שהיינו רוצים בדיוק 200 דוגמאות, 100 חיוביות (שרדו, שורה 1) ו-100 שליליות (לא שרדו, שורה 2), אבל היא מתירה לנו גמישות בתוך תת-קבוצת החיוביים: למשל, מתוך ה-100 השליליים לא אכפת לנו כמה נשים יהיו, ובלבד שיהיו בתחום 48-52 (שורה 3; ואותו דבר בחיוביים, שורה 4). שורה 11, למשל, אומרת שמבין הנשים שלא שרדו אנחנו מבקשים גם 8-12 נוסעות ממחלקה ראשונה.

הכלי שבנינו, שמופץ בחבילת פייתון בשם curation_magic, מקבל שתי טבלאות כאלה, ותוך שניות מחזיר סט של דוגמאות שעומד – עד כמה שאפשר בקירוב – בכל הדרישות. הקוד שלו פתוח ואתם יכולים להשתמש בו.

איך זה עובד?

כדי לפתור את הבעייה ניסחנו אותה כבעיית "תכנון לינארי" – משימה שבה צריך למצוא השמה אופטימלית לצירוף לינארי של משתנים, תחת אוסף אילוצים על המשתנים הללו שגם אותו ניתן לנסח באופן לינארי. עבור בעיות שמצליחים לנסח כך יש לנו היום מרשם בדוק שמאפשר למצוא עבורן את ההשמה האופטימלית בשניות ספורות (או להתריע שאין אף השמה שעומדת בכל האילוצים), והוא ממומש במגוון חבילות פייתון, למשל scipy.

במקרה שלפנינו, נניח שיש לנו N דוגמאות (בטבלה הראשונה) ו-M תנאים (בטבלה השנייה).

איך נגדיר את המשתנים? נגדיר משתנה $x_i$ לכל אחת מהדוגמאות 1..N. אנחנו רוצים ש- $x_i$ יהיה 1 אם דוגמה i מיועדת להיכלל בקבוצת המדגם, ו-0 אם לא. כעת ניתן להפוך כל שורה בטבלת התנאים לאילוץ על צירוף לינארי של x-ים. למשל, עבור התנאי האחרון (age >=40), אנחנו רוצים שיהיו בין 48 ל-52 נציגים בקבוצת המדגם הסופית. ניקח את כל ה-xים שהדוגמאות שלהם עומדות בתנאי הזה; הסכום שלהם צריך להיות בין 48 ל-52. כך:

$48 \leq \left(\sum_{i: age(i) \geq 40}x_i\right)\leq 52$

אם ניצור משתי הטבלאות מטריצה A בגודל M על N, כך ש-Aji שווה 1 אם דוגמה i מקיימת את תנאי j (ו-0 אחרת) נוכל לרשום את כל האילוצים הללו בכתיב מטריציוני:

$b_{min}\leq Ax \leq b_{max}$

כאשר $b_{min}$ ו- $b_{max}$ מתייחסים לטורים בשם זה בטבלת התנאים שלעיל.

בעייה 1: מה אם אין פתרון?

הבעייה האמיתית היא שהאילוצים מייצגים את האידאל, שאינו בהכרח ניתן להשגה. התוכנית הנ"ל תודיע ש"אין פתרון" במידה והיא לא יכולה לעמוד באחד התנאים שהכתבנו. במקרה זה, נצטרך להשקיע זמן רב בהבנה של מהו התנאי הבעייתי, ובשינוי החסמים עבורו. בפועל, אם יש חריגות קטנות מהתנאים שהצבנו בהתחלה, זו לא בהכרח בעייה משמעותית, ונוכל להתמודד איתה.

נרצה לפיכך להתאים את התוכנית שלנו, כדי לתת לה יותר חופש פעולה לחרוג (בקצת) מדי פעם מאחד התנאים. לכל תנאי i נוסיף משתנה חדש $c_j$ שמייצג את החריגה מהתנאי הזה (נאלץ אותו להיות אי-שלילי ( $c_j \geq 0$ ) – זהו גם אילוץ לינארי), פונקציית המטרה שלנו תהיה צמצום סך כל החריגות. באופן זה נוכל להיות בטוחים שתמיד יימצא פתרון שיעמוד בכל האילוצים – כי כעת יהיה מותר לחרוג מהם.

לצורך כך, האילוץ שכתוב למעלה ישתנה להיות:

$48-c_{15} \leq \left(\sum_{i: age(i) \geq 40}x_i\right)\leq 52 + c_{15}$

( $c_{15}$ כי השורה האחרונה בטבלה 2 היא שורה 15). אם $c_{15}=0$ ואי-השיוויון לעיל מתקיים, אז למעשה זה אומר שההשמה שנתנו ל-xים עומדת בתנאי 15 המקורי, ללא חריגות. אבל גם אם לא, אם נגדיל את $c_{15}$ מספיק, מתישהו אי-השיוויון הזה, על שני צדדיו, יתחיל להיות נכון. לכן, כאשר מוסיפים את משתני ה-c, העבודה של התוכנית הליניארית עוברת מלמצוא פתרון פיזיבילי (כזה שעומד בכל התנאים המקוריים), לצמצום כמות החריגות מהם.

התוכנית הלינארית המלאה, בכתיב מטריציוני, תיראה כך:

LP1

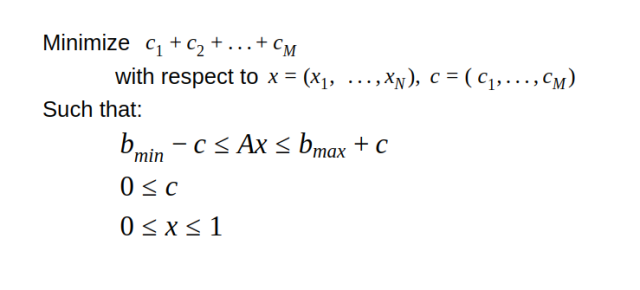
בעייה 2: מפיתרון שבור לפיתרון שלם

הפתרון של התוכנית הלינארית (שהמחשב מוצא) מציב ערכים בכל משתני ה- $x_i$ , כלומר אחד לכל דוגמה. הערכים האלה חייבים להיות בין 0 ל-1 (כי זה אחד האילוצים בתוכנית). אבל אם $x_i=0.24$ , מה זה אומר לגבי הדוגמה ה-iית? האם היא תיכלל בקבוצת המדגם או לא?

הדרך הכי נאיבית להחליט היא פשוט לעגל את ה- $x_i$ -ים, ככה שהם הופכים להיות ערכים בינאריים, או 0 או 1, ולקחת לקבוצת המדגם את כל הדוגמאות שעבורן $x_i$ הוא 1. זה אומר שהפתרון שנקבל הוא כבר לא בדיוק אותו פתרון אופטימלי שעשה אופטימיזציה לתוכנית הליניארית, אלא קירוב שלו, וברוב המקרים זה לא יהיה קירוב כזה גרוע (בדרך כלל הרבה מה- $x_i$ -ים יהיו גם ככה 0 או 1, עוד לפני העיגול).

בעייה 3: מאילוצים אבסולוטיים לאילוצים יחסיים

לעיתים האילוצים בטבלה 2, שעבור כל חתך נותנים חסמים על מספר הדוגמאות בחתך, הם לא מספיק משוכללים. למשל, נניח שאנחנו נותנים טווח רחב למספר הדוגמאות השליליות (נגיד בין 90 ל-110), אבל היינו רוצים שלפחות 30% מהדוגמות השליליות יהיו ממחלקה שנייה (Pclass=2). נוכל בקלות להציב חסמים של 90 ו-110 על התנאי [Survived==0], אבל איזה חסמים נשים על התנאי [Pclass==2 & Survived==0]? בשעת הגדרת החסמים עוד לא ידוע לנו כמה דוגמאות שליליות תיכנסנה לקבוצת המדגם — זה יכול להיות כל מספר בין 90 ל-110 (ואף מעבר כי אנחנו מאפשרים חריגות) — ולכן 30% מזה יכול להיות כל מספר בין 27 ל-33. איזה מספר נבחר?

היינו רוצים לאפשר למשתמש לתת חסמים יחסיים:

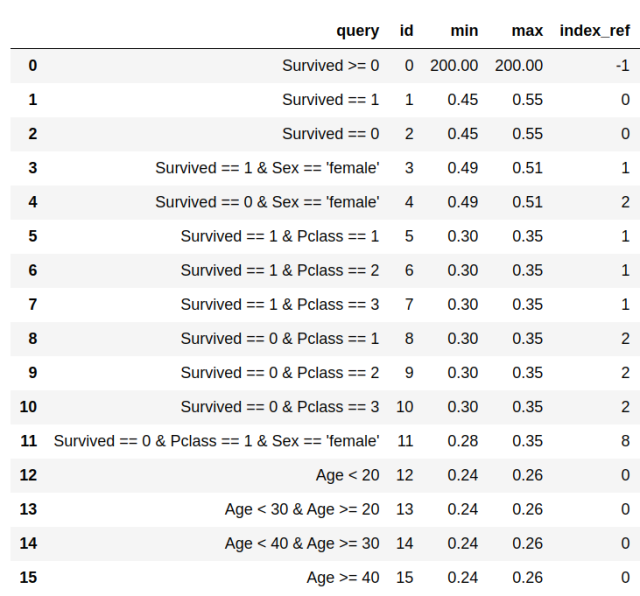
טבלה 3: אותם האילוצים כמו טבלה 2, אך מובעים כעת באופן יחסי. לכל שאילתא מופיעה הכמות המותרת של נוסעים שיכולים להיכלל בקבוצת המדגם, כחלק היחסי מקבוצת הנוסעים שעומדים בתנאי שאילתא קודמת שמספרה מופיע בטור index_ref.

לדוגמה, שורה 9 בטבלה 3, אומרת שמספר הדוגמאות שעבורן [Survived==0 & Pclass==2] יהוה 30-35% ממספר הדוגמאות שמקיימות את התנאי בשורה 2 [Survived==0], או במילים אחרות שמבין הנוסעים שלא שרדו מספר הנוסעים ממחלקה 2 צריך להיות 30-35%. כעת אנחנו יכולים להציב את התנאי הזה מבלי לדעת מראש כמה דוגמאות שליליות יהיו לנו. אם יהיו 110, אז האלגוריתם ינסה למצוא לנו לפחות 33 נוסעים שלא שרדו ממחלקה 2, ואם יהיו 90, האלגוריתם יוכל להסתפק ב-27.

לשימחתנו, גם בתוספת האילוצים ה"יחסיים" הללו, ניתן לנסח את הבעייה כבעיית תכנון ליניארי, והוספנו לחבילת curation_magic אפשרות לתת את האילוצים גם באופן הזה. הנה התשובה שנתנה המערכת לאילוצים שבטבלה 3:

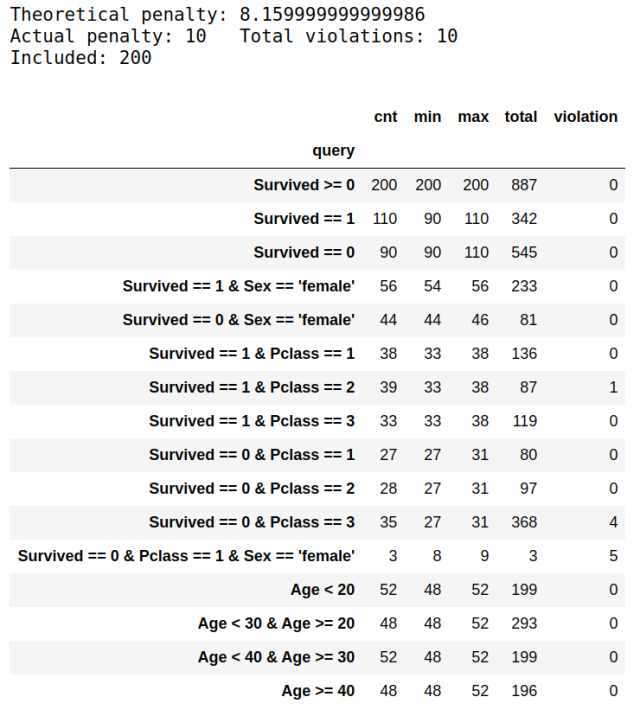
טבלה 4: תוצאות איכלוס קבוצת המדגם. באיזה אילוצים עמדנו?

ניתן לראות שאכן המערכת ניצלה את החופש שלה ובחרה יותר שורדים (110) מלא-שורדים (90), ועדיין עמדה במירב האילוצים שיכלה בכל תת-קבוצה. ניתן גם לראות שיש פער בין הפתרון האופטימלי (השבור) שמצאה התוכנית הלינארית (8.16), לבין הפתרון בשלמים (10).

הרחבה נוספת (ופשוטה) שניתן לעשות היא להגדיר עונש שונה להפרה של כל אילוץ. מי שמעניין אותו לראות איך מגדירים את הבעייה במקרה זה, והרחבות נוספות, מוזמן להסתכל ב-notebook שפרסמנו ב-github. מקווה שיהיה מעניין ושימושי.

תוכניות לינאריות ואיך בונים קבוצת מדגם

2 תגובות על תוכניות לינאריות ואיך בונים קבוצת מדגם

כתיבת תגובה לבטל

פוסטים אחרונים

ארכיון

קטגוריות

כלים

לעקוב אחרי הבלוג באימייל

תוכניות לינאריות ואיך בונים קבוצת מדגם

שתף

קשור

2 תגובות על תוכניות לינאריות ואיך בונים קבוצת מדגם

כתיבת תגובה לבטל

פוסטים אחרונים

ארכיון

קטגוריות

כלים

לעקוב אחרי הבלוג באימייל